A matemática desempenha um papel fundamental na descrição e compreensão dos fenômenos físicos que ocorrem ao nosso redor. Um teorema importante no campo da matemática aplicada à Física e Engenharia é o Teorema da Divergência, também conhecido como Teorema de Gauss. Neste artigo, exploraremos o conceito do Teorema da Divergência, sua formulação matemática e algumas aplicações práticas em diferentes áreas científicas.
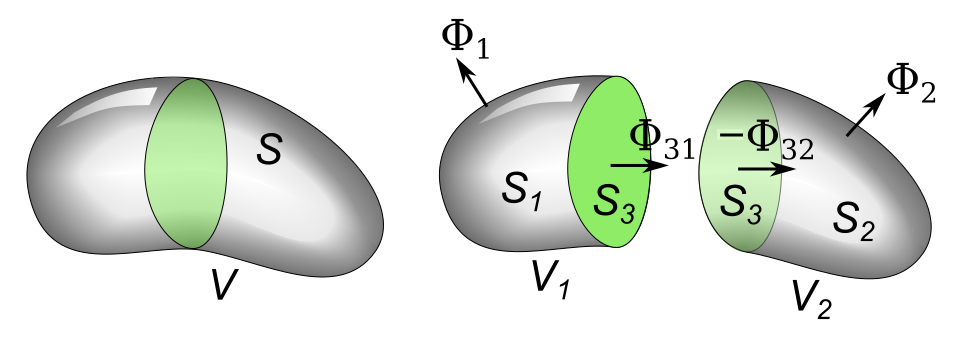
O Teorema da Divergência: O Teorema da Divergência é uma relação fundamental entre fluxos e divergências de campos vetoriais em três dimensões. Matematicamente, ele estabelece uma conexão entre uma integral de volume de uma função vetorial e uma integral de superfície que circunda esse volume. A formulação matemática do teorema é dada por:
$$\iiint_V \nabla \cdot \mathbf{F} \, dV = \iint_S \mathbf{F} \cdot d\mathbf{S}$$
Onde:
- \(\mathbf{F}\) é um campo vetorial contínuo definido em uma região \(V\) do espaço tridimensional,
- \(\nabla \cdot \mathbf{F}\) é a divergência de \(\mathbf{F}\),
- \(dV\) é um elemento de volume em \(V\),
- \(S\) é a superfície fechada que envolve \(V\),
- \(\mathbf{F} \cdot d\mathbf{S}\) é o produto escalar entre \(\mathbf{F}\) e o vetor diferencial de área \(d\mathbf{S}\) apontando para fora da superfície \(S\).
Aplicações do Teorema da Divergência:
1. Eletromagnetismo:
O Teorema da Divergência é usado extensivamente no estudo do Eletromagnetismo. Por exemplo, na Lei de Gauss para o campo elétrico, o teorema é aplicado para relacionar a carga total contida em um volume a um fluxo elétrico através de uma superfície fechada que envolve esse volume. Isso permite a análise de distribuições de cargas elétricas.
2. Mecânica dos Fluidos:
A Mecânica dos Fluidos é outra área onde o Teorema da Divergência encontra aplicações significativas. Na equação de continuidade, o teorema é utilizado para relacionar o fluxo de massa de um fluido incompressível através de uma superfície fechada à sua divergência em um determinado volume. Isso permite o estudo do fluxo e transporte de fluidos em sistemas complexos.
3. Transferência de Calor:
Na área da Transferência de Calor, o Teorema da Divergência é usado para derivar as equações de conservação de energia térmica. Ele relaciona o fluxo de calor através de uma superfície com a variação da temperatura no interior de um sólido ou fluido. Essa aplicação é essencial na análise de processos de transferência de calor em engenharia e na modelagem de sistemas térmicos.
4. Análise de Campo de Velocidade:
Em mecânica dos fluidos e aerodinâmica, o Teorema da Divergência é empregado para analisar campos de velocidade de fluidos. Ele permite a análise do fluxo de fluidos através de uma superfície fechada e relaciona isso com a divergência do campo de velocidade no interior do volume. Essa aplicação é útil na determinação de fluxos de fluidos, como em torno de corpos sólidos ou em sistemas de escoamento.
O Teorema da Divergência é uma ferramenta matemática poderosa usada na Física e Engenharia para relacionar fluxos e divergências de campos vetoriais em três dimensões. Sua aplicação em diversas áreas científicas, como Eletromagnetismo, Mecânica dos Fluidos e Transferência de Calor, demonstra sua importância na análise e compreensão dos fenômenos naturais e no desenvolvimento de tecnologias. Ao utilizar o Teorema da Divergência, os cientistas e engenheiros podem desvendar os segredos dos campos físicos e desenvolver soluções inovadoras para uma ampla gama de problemas práticos.
Aqui estão algumas referências que você pode utilizar para aprofundar o conhecimento sobre o Teorema da Divergência e suas aplicações:
1. Arfken, G. B., Weber, H. J., & Harris, F. E. (2012). Mathematical Methods for Physicists: A Comprehensive Guide. Academic Press.
2. Griffiths, D. J. (2017). Introduction to Electrodynamics. Cambridge University Press.
3. Çengel, Y. A., & Cimbala, J. M. (2014). Fluid Mechanics: Fundamentals and Applications. McGraw-Hill Education.
4. Incropera, F. P., DeWitt, D. P., Bergman, T. L., & Lavine, A. S. (2017). Fundamentals of Heat and Mass Transfer. Wiley.
5. Batchelor, G. K. (2000). An Introduction to Fluid Dynamics. Cambridge University Press.
6. Duan, Z., & Zhang, J. (2017). Mathematical Analysis and Applications: From Differential Equations to Fourier Series and Wavelets. Springer.
7. Hassani, S. (2013). Mathematical Physics: A Modern Introduction to Its Foundations. Springer.
Lembrando que é sempre importante verificar as referências específicas para cada área de aplicação do Teorema da Divergência, conforme necessário.